Correlation is the basis of superstition and causation the foundation of science.
Anonymous
As investors deciding to invest in an economy care for the country’s GDP growth, uncertainty about its magnitude can affect investment. Therefore, the recent debate about India’s GDP growth rates following the revision in India’s GDP estimation methodology in 2011 assumes significance, especially given the recent slowdown in the growth rate. Using careful statistical and econometric analysis that does justice to the importance of this issue, this chapter finds no evidence of mis-estimation of India’s GDP growth. The chapter starts from the basic premise that countries differ among each other in various observed and unobserved ways. Therefore, cross-country comparisons are fraught with risks of incorrect inference due to various confounding factors that stem from such inherent differences. As a result, cross-country analysis has to be carefully undertaken so that correlation is distinguished from causality. The models that incorrectly over-estimate GDP growth by 2.77 per cent for India post-2011 also mis-estimate GDP growth over the same time period for 51 other countries out of 95 countries in the sample. The magnitude of mis-estimation in the incorrectly specified model is anywhere between +4 per cent to -4.6 per cent, including UK by +1.6 per cent, Germany by +1.0 per cent, Singapore by -2.3 per cent, South Africa by -1.2 per cent and Belgium by -1.3 per cent. Given the lower growth rates for UK and Germany compared to India, the mis-estimation in percentage terms in the incorrectly specified model is much larger for UK (76 per cent) and Germany (71 per cent) than for India (40 per cent). However, when the models are estimated correctly by accounting for all unobserved differences among countries as well as the differential trends in GDP growth across countries, GDP growth for most of these 52 countries (including India) is neither over- or underestimated. In sum, concerns of over-estimation of India’s GDP are unfounded.
The larger point made by this chapter needs to be understood by synergistically viewing its findings with the micro-level evidence in Chapter 2, which examines new firm creation in the formal sector across 504 districts in India. Two observations are critical. First, the granular evidence shows that a 10 per cent increase in new firm creation increases district-level GDP growth by 1.8 per cent. As the pace of new firm creation in the formal sector accelerated significantly more after 2014, the resultant impact on district-level growth and thereby country-level growth must be accounted for. Along these lines, Purnanandam (2019) shows that India’s improvement in indicators such as access to nutrition and electricity might explain the higher growth rate in Indian GDP post the methodological change. Second, granular evidence on new firm creation shows that new firm creation in the Service sector is far greater than that in manufacturing, infrastructure or agriculture. This micro-level evidence squares up fully with the well-known macro fact on the relative importance of the Services sector in the Indian economy. The need to invest in ramping up India’s statistical infrastructure is undoubted. In this context, the setting up of the 28-member Standing Committee on Economic Statistics (SCES) headed by India’s former Chief Statistician is important. Nevertheless, carefully constructed evidence in the Survey must be taken on board when assessing the quality of Indian data.
INTRODUCTION
10.1 To achieve the objective of becoming a USD 5 trillion economy by 2025, a strong investment climate is critical. The Economic Survey of 2018-19 laid out the role of investment, especially private investment, in driving demand, creating capacity, increasing labour productivity, introducing new technology, allowing creative destruction, and generating employment. Undoubtedly, investment assumes primacy in catalyzing the economy into a virtuous cycle.
10.2 In recent times, India has taken several initiatives to foster investment, be it relaxing FDI norms, cutting corporate tax rates, containing inflation, accelerating infrastructure creation, improving ease of doing business, or reforming taxation. Investors, including international investors, see an unparalleled opportunity in India as it is one of the fastest growing large economies in the world. The growth rate of the economy is a pre-eminent driver of investment decisions. Moreover, the level and growth rate of a country’s GDP informs several critical policy initiatives by serving as a barometer of the economy’s size and health.
10.3 In recent times, there has been significant debate about the veracity of India’s GDP growth rates, with particular focus being placed on these growth rates following the change in the GDP estimation methodology in 2011-12 (see Box 1 for a note on the revision). Both national and international experts including Bhalla (2019), Goyal and Kumar (2019), Roy and Sapre (2019), Panagariya (2019), Purnanandam (2019), Subramanian (2019) and Vaidya Nathan (2019) have contributed to the debate on whether the GDP growth rates in India are correctly estimated or not. As concerns about the veracity of India’s GDP growth rates may generate substantial concerns not only to investors but also to policymakers, this issue warrants a careful examination. Such an examination is important especially given the slowdown in the GDP growth rates over recent quarters. If investors apply a “discount” to a lower growth rate, even if incorrectly, the same can really affect investor sentiment. This chapter, therefore, studies this important issue.
10.4 The aim of the chapter is to estimate the inaccuracy, if any, in the GDP growth rate using the difference-indifference methodology as implemented in Subramanian (2019) and Purnanandam (2019). Estimating the inaccuracy of any measured variable requires a benchmark for the “accurate estimate”, which by definition represents a “counter-factual”, i.e. one that is not revealed in fact and therefore has to be estimated. This assessment is undertaken by comparing the Indian GDP growth rates to those of other countries. Effectively, this methodology asks the question “what would have been the estimate of the Indian GDP growth rate if the methodological change had not been implemented” and compares this estimate to the actual growth rate to infer the incorrectness in the estimates.
Box 1: Change in the Base Year of the GDP Series
The Base Year of the GDP Series was revised from 2004-05 to 2011-12 and released on 30 January, 2015 after adaptation of the sources and methods in line with the System of National Accounts (SNA) 2008 of the United Nations. The methodology of compilation of macro aggregates was finalized by the Advisory Committee on National Accounts Statistics (ACNAS) comprising experts from academia, National Statistical Commission, Indian Statistical Institute (ISI), Reserve Bank of India (RBI), Ministries of Finance, Corporate Affairs, Agriculture, NITI Aayog and selected State Governments. The decision taken by the Committee was unanimous and collective after taking into consideration the data availability and various methodological aspects.
For the purpose of global standardization and comparability, countries follow the SNA evolved in the UN after elaborate consultation. The SNA 2008 is the latest version of the international statistical standard for the national accounts, adopted by the United Nations Statistical Commission (UNSC) in 2009 and is an update of the earlier 1993 SNA. The Inter-Secretariat Working Group on National Accounts (ISWGNA) in India was mandated to develop the 2008 SNA through intense discussions and consultation with member countries. India also participated in the deliberations of the Advisory Expert Group. In its adoption of the 2008 SNA the UNSC encouraged Member States, regional and sub-regional organizations to implement its recommendations and use it for the national and international reporting of national accounts statistics based on the available data sources.
10.5 This methodology is similar to ones that researchers in medicine use to estimate whether a drug is effective or not. For concreteness, think of testing a drug for blood pressure (BP). Create two groups of identical guinea pigs – a treatment group that is administered the drug and a control group that is given sugar pills. Identical groups ensure apples-to-apples, instead of apples-to-oranges, comparison. When the groups are identical, before-after difference in BP for treatment group minus the same difference for control group estimates the correct effect of the drug by removing any confounding placebo effects. Effectively, the change in BP for the control group asks the question “what would have been the change in BP even if the drug had not been administered?” This methodology that researchers call “difference-in-difference” is used extensively in economic research.
10.6 In the context of GDP growth rate estimation, India represents the treatment group and other countries represent the control group. Countries differ from each other in ways that can be measured and, especially, in ways that cannot be measured; both sets of differences can affect economic activity. Therefore, cross-country comparisons are fraught with risks of incorrect inference due to various confounding factors that stem from such inherent differences. As a result, cross-country analysis has to be carefully undertaken so that correlation is distinguished from causality. So, researchers using data across several countries implement careful statistical techniques, called panel-data econometrics, to ensure an apples-to-apples comparison across countries and thereby mimic the above example of testing a drug’s effectiveness on BP.
10.7 Using careful statistical and econometric analysis that does justice to the importance of this issue, no evidence of misestimation of India’s GDP growth is found. Indeed, the models that incorrectly overestimate GDP growth by over 2.77 per cent for India post-2011 also mis-estimate GDP growth over the same time period for 51 other countries by any where between +4 per cent to -4.6 per cent, including UK by +1.6 per cent, Germany by +1.0 per cent, Singapore by -2.3 per cent, South Africa by -1.2 per cent and Belgium by -1.3 per cent. However, when the models are estimated correctly by accounting for all unobserved differences among countries as well as the differential trends in GDP growth across countries, GDP growth for most of these 52 countries is neither over- or under-estimated. In sum, concerns of overestimation of India’s GDP are unfounded.
10.8 The analysis is concludedby examining other signs that may indicate a problem with the GDP estimation methodology. As in Subramanian (2019), the GDP growth rates are correlated with other indicators that have not undergone any changes in methodology. In essence, the methodology involves correlating the “suspect” variable – the GDP growth rate – with several other “reliable” variables to uncover any suspicious patterns. As in Subramanian (2019), these “reliable” variables include exports, imports, real credit to industry, petroleum consumption, railway freight traffic, electricity consumption, etc. This diagnostic exercise is undertaken while recognizing that correlations can be non-stationary, i.e., can vary over time due to factors that may be unrelated to the change in the GDP methodology.
10.9 The results clearly establish the concern that the correlations studied as a diagnostic for GDP growth are notoriously non-stationary: not only do they flip signs frequently over various 3-year or 5-year time periods from 1980 to 2015, their values change significantly over this time period as well. Given such change in the correlations for reasons unrelated to the specific change in the GDP methodology in 2011, there seems to be no cause for concern regarding the mis-estimation of India’s GDP. Further, the relationship of these indicators with the new GDP series does not diverge from their relationship with the old series. In other words, the relationship between these indicators and GDP is preserved even after the methodology revision, thereby adding to the evidence that the revised methodology estimates the GDP correctly.
IS GDP MISESTIMATED?
The Choice of Model: Is the Standard Difference-in-Difference Appropriate?
10.10 Cross-country data is gathered from the World Bank’s World Development Indicators (WDI) database as in Purnanandam (2019) and Subramanian (2019). The sample exclude oil exporters1, countries with population less than 1 million, and war-torn and politically fragile countries, in line with Subramanian (2019). Although the sample is unlikely to be an exact replica of these papers’ samples, hence, a substantial overlap2 is expected. In any case, this chapter aims to test the robustness of results to an independent verification, among other objectives. A sample that varies slightly from the original serves as a check of robustness to sample selection.
10.11 The standard difference-in-difference (DID) model is an econometric technique that attempts to mimic an experimental research design by studying the differential effect of a quasi-experiment such as a GDP methodology change. The differential effect studied is the difference in average GDP growth rate in a country that has gone through the methodology change, such as India (treatment group), versus other countries which have not gone through the change (control group). See Box 2 for a note on this methodology.
Box 2: A Note on the Difference-in-difference Method

This version of DID calculation subtracts the average GDP growth rate difference before the GDP methodology change (pre-treatment difference) between India and the controls from the average GDP growth rate difference after the GDP methodology change (post-treatment difference), thereby adjusting for the fact that GDP growth rates in India and the rest of the other countries used as controls in the chapter were not the same initially.
DID logic is depicted in Figure 1 which plots the GDP growth of India and the control countries for the period 2002-2011 (Before) with the period 2012-2016 (After) by a solid line. The DID tool amounts to a comparison of trends in average GDP growth between India and other control countries. The dotted line in the figure is the counterfactual outcome that lies at the heart of the DID research design. This dotted line indicate what would have happened to GDP growth estimation without the GDP methodology change and more crucially if everything evolved in India as it did with the control countries i.e., the GDP growth rates moved parallelly between India and the control countries.
The DID counterfactual comes with an easily stated but even so, a formidable assumption of common trends. In the GDP methodology quasi-experiment, DID presumes that, absent any GDP methodology change, the average GDP growth trend in countries used as controls in the chapter is what one should expect to see in India as well. This assumption requires that before the “treatment” in 2011, India and the other countries followed a parallel trend in GDP growth – one that would have continued had India not been “treated” to a methodology revision. This assumption can seen from Figure 2 does not hold good. Notwithstanding the fact that DID is only an imperfect model to estimate GDP overstatement, this chapter nevertheless employs the methodology, with caveats, for comparability with other studies on the subject.
Figure 1: Illustration of the treatment effect in an ideal difference-in-difference design
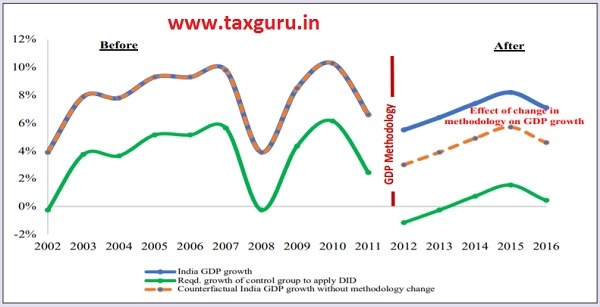
Source: World Bank WDI Database.
Figure 2: India and other countries did not follow a parallel trend before the “treatment” before 2012, making DID an imperfect model to measure mis-estimation
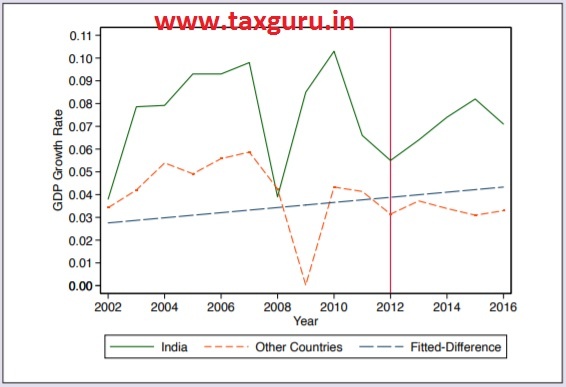
Source: World Bank WDI Database.
10.12 A fundamental assumption required for the standard DID model to correctly measure the magnitude of mis-estimation in GDP growth is the “parallel trends” assumption. In the GDP methodology quasi-experiment, DID presumes that, absent any GDP methodology change, the average GDP growth trend in countries used as controls in the chapter is what one should expect to see in India as well. This assumption requires that before the “treatment” in 2011-12, India and the other countries followed a parallel trend in GDP growth – one that would have continued had India not been “treated” to a methodology revision. Only then one can do an apples-to-apples comparison. If the parallel trends assumption is violated, then the standard DID is not an appropriate tool for the current problem (see Box 2 for an illustration of the parallel trends assumption).
10.13 Figure 3, derived from Purnanandam (2019), compares in the two panels respectively, a) India’s growth trajectory with all other sample countries, b) India’s trajectory with the average for other middle income countries in the sample. Figure 4 plots the trajectories of India against other middle income countries individually until the year of methodology revision, 2011-12. All charts make it clear that India and the other countries did not follow a parallel trend in growth before 2011. Even when compared to other Asian middle income countries (the first panel of Figure 4), the analysis fail to see parallel trends. There is not only variation between the treatment and control groups, but also variation within the control group.
Figure 3: India and other countries do not follow a parallel trend in GDP growth prior to 2011
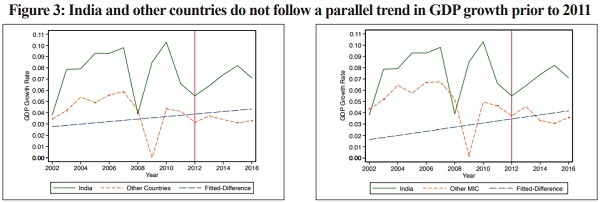
Source: Purnanandam (2019)
Figure 4: India and other middle income countries do not follow a parallel trend in GDP growth prior to 2011
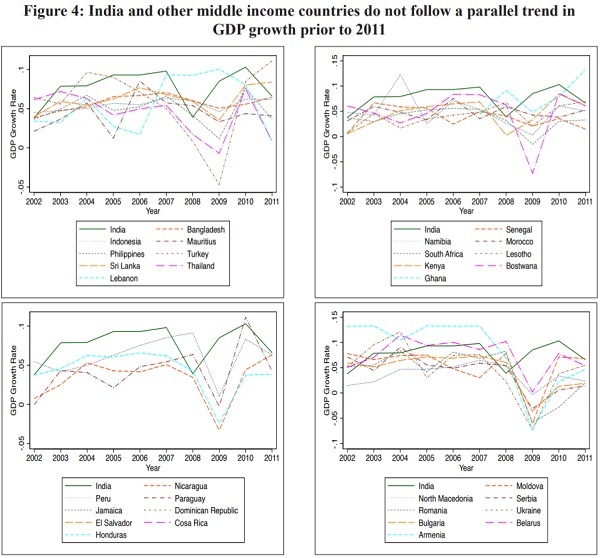
Source: World Bank WDI Database.
10.14 The parallel trends assumption is critical for any inference from a standard DID model. However, as the figures make clear, India did not follow a parallel trend compared to other countries prior to 2011, so there is no reason to assume that India would have continued on a parallel trend after 2011 in the absence of a methodology revision, and the measured difference-in-difference (treatment effect of the 2011 revision) should therefore be treated with caution.
10.15 The other challenge is the choice of independent variables. As GDP is an immensely complex phenomenon that is influenced directly and indirectly by a range of socio-economic factors, some of which are measured and most of which are non-measurable, there is a high risk of omitted variable bias – an issue considered in the next section.
10.16 The lack of a parallel trend between the treatment and control, as well as the possibility of omitted variable bias, render the standard DID methodology an imperfect tool to evaluate whether India’s GDP is misestimated. Nevertheless, to begin with, a baseline standard DID model is estimated as implemented in Sub-ramanian (2019). In order to bring out comparability with other studies such as Sub-ramanian (2019). In subsequent sections, various ways are explored to adjust the model to overcome these limitations.
10.17 The following cross-sectional regression is estimated twice, once for the pre-change period and once for the post-change period:
![]()
The dependent variable is the real GDP growth rate of country i in period T. The independent variables include real growth rates of exports, imports and credit to the private sector, as well as a dummy for India. For each country, the continuous variables are averaged over all pre-change years for the first estimation, and over all post-change years for the second estimation. The coefficient of interest is the Indiai dummy. The difference between the coefficient from the post-change specification and the pre-change one gives the magnitude of mis-estimation in the post-change period.
10.18 The two pooled cross-sectional regressions above can be clubbed into one specification as follows:
![]()
In this model, the treatment period is captured by T, which equals one for the post-change period and zero for the pre-change period. The variable of interest now is θ2 which captures the level of mis-estimation of the Indian GDP post-change.
10.19 Table 1 presents results. Using this rudimentary specification, it was found that India’s GDP was overstated by 2.77 percent. Results mirror the results of Subramanian (2019), who finds an overestimation of 2.5 per cent. Further, the analysis considered the issues associated with this model and implementation adjustments. After making these adjustments, the evidence in favour of a misestimated GDP weakened considerably.
Table 1: Estimation of abnormal growth in GDP using a cross-country standard DID model
| Dependent variable: Average GDP growth |
2002-11 | 2012-16 | Pooled |
| India | 0.0092**
(2.4151) |
0.0369***
(15.7342) |
0.0092**
(2.4151) |
| India x Post-Change | 0.0277***
(6.1757) |
||
| Post-Change | 0.0042
(1.0690) |
||
| Export Growth Rate | 0.0929*
(1.9697) |
0.0805**
(2.1591) |
0.0929*
(1.9697) |
| Import Growth Rate | 0.1856***
(3.3672) |
0.0225
(0.6245) |
0.1856***
(3.3672) |
| Credit Growth Rate | 0.0632***
(3.3336) |
0.1892***
(6.4593) |
0.0632***
(3.3336) |
| Export Growth x Post-Change | -0.0125
(-0.2075) |
||
| Import Growth x Post-Change | -0.1631**
(-2.4767) |
||
| Credit Growth x Post-Change | 0.1260***
(3.6123) |
||
| Constant | 0.0139***
(4.3905) |
0.0181***
(7.7800) |
0.0139***
(4.3905) |
| Observations R2 | 95
0.5323 |
95
0.5304 |
190
0.5443 |
Note: Columns 1 and 2 estimate the following cross-sectional regression:
![]()
For each country i, the dependent and independent variables are averaged over the period 2002-11 and 2012-16 in columns 1 and 2 respectively. Column 3 pools the observations from both periods and estimates the following regression: giT=β0 +β1Xi+β1Xi×T+θ1Indiai+θ2Indiai×T+γT+εiT . gi equals the average growth rate for country i in either 2002-11 or 2012-16 period. T equals one for the post-change period and zero otherwise. India equals one for India and zero for all other countries. t-statistics are provided in parentheses. *, ** and *** denote significance levels of 10 per cent, 5 per cent and 1 per cent respectively3.
Choice of Covariates: A Generalized DID to Handle Omitted Variable Bias
10.20 The omission of important variables in a regression model can lead to what is known as omitted variable bias (see Box 3). For example, the regression attempted above excludes important agriculture- and services-related indicators as well as other unobserved factors that may affect GDP growth. To illustrate the effect of omitted variable bias on the results, the analysis re-estimate rudimentary baseline model with different combinations of independent variables:
![]()
In particular, besides the existing covariates – real growth in exports, imports and credit – real growth in agriculture and real growth in services were added to the model. Table 2 presents results. Column 1 indicates the baseline estimation in which India’s GDP growth appears overstated by 2.77 percent, as earlier. Column 2 includes real services growth in the model, which yields a much lower mis-estimation of 1.18 per cent. Moreover, the coefficient of interest in this case is only weakly statistically significant. Column 3 includes real agriculture growth in the model, which causes the mis-estimation to drop to 2.6 per cent. Column 4 includes both agriculture and services growth, which also causes the mis-estimation to drop further to 1.1 per cent. The final column runs a model with only the agriculture and services indicators and finds the level of misestimation to be negative.
10.21 The objective of Table 2 is not to provide a refined estimate of the level of misestimation, but to illustrate the extremely high sensitivity of the findings to the choice of covariates used in the model. Clearly, the baseline model with only three covariates significantly overestimates the level of overestimation.
Box 3: A note on omitted variable bias in regression models
Regression is a statistical technique, which if done the right way, is a way to make other things equal by controlling for or removing the effects of variables (such as indicators from the services, industrial and agriculture sectors of the economy) that are related to the dependent variable (such as GDP growth rate). One may be interested in the effect on GDP growth rate from a GDP methodology change and not particularly interested in the variables from the services, industrial and agriculture sectors of the economy. But equality is established only for the variables included as controls. Failure to include enough controls or the right controls gives biased results from the regression. This bias in the results is called Omitted Variable Bias (OVB).
Suppose the following ‘short’ regression does not have either enough controls or the right controls:
![]()
where GDP denotes the GDP growth in a particular country in a given year, αS is the intercept of the short regression, β1S is the regression coefficient of X1, X1 is a vector of independent variables in the ‘short’ regression of say industrial indicators and consequently does not have enough/right controls for GDP growth, βS is the causal effect estimated of the GDP methodology change on GDP growth rate, XIndia is the India country dummy and εS is the residual or the error term.
Now, suppose following ‘long’ regression is run such that it has enough/right controls:
![]()
where αL is the intercept of the long regression, β2L is the regression coefficient of X2, X2 is a vector of omitted controls, βL is the causal effect estimated of the GDP methodology change on GDP growth rate, and εL is the residual.
The bias in the estimation of GDP growth rate from methodology change due to omitted variables is:
![]()
where π1 is the coefficient of the following regression:
![]()
The illustration below summarizes the direction of the omitted variable bias. The dependent variable is GDP, X1 and X2 are the independent variables, and X2 is the omitted variable.
X1 and X2 are positively X1 and X2 are negatively
correlated correlated
X2 has a positive effect on GDP Positive bias Negative bias
X2 has a negative effect on GDP Negative bias Positive bias
For example, with regard to the study by Subramanian (2019) that aimed to explain GDP growth using indicators of real economic activity, the Economic Advisory Council recently wrote, “a cursory look at the indicators suggests a strong link with industry indicators (a sector that contributes an average of 22 per cent to India’s GDP), while the representation of services (60 per cent of GDP) and agriculture (18 per cent of GDP) is as good as missing. It is difficult to believe that indicators in the services sector would not correlate with Indian GDP.” (Economic Advisory Council to the Prime Minister, 2019)
In the above analysis, say X1 indicates the manufacturing-related indicators and X2 represents the missing indicators from services and agriculture. The indicators from industry are expected to be positively correlated with that of services and agriculture, so X1 and X2 are positively correlated. Similarly, the missing indicators from services and agriculture will have a positive effect on GDP growth rate. So, omitted variable bias is expected to be positive. Notwithstanding the fact that DID is an imperfect model to estimate GDP overstatement, the overestimation of 2.5 per cent found in Subramanian (2019) is itself likely to be overestimated because of omitted variable bias, as the explanatory variables (exports, imports and credit) do not adequately cover all the sources of variation in GDP growth.
Table 2: Illustration of the effect of omitted variable bias on level of mis-estimation
| Baseline | Incl. services | Incl. agri. | Incl. both services & agri. |
Excl. exports, imports, credit |
|
| India x Post-Change | 0.0277***
(6.1757) |
0.0118*
(1.9719) |
0.0261***
(5.7183) |
0.0112**
(2.1128) |
-0.0090**
(-2.0210) |
| India | 0.0092**
(2.4151) |
0.0059*
(1.8999) |
0.0087**
(2.2617) |
0.0066**
(2.4470) |
0.0173***
(7.4551) |
| Post-Change | 0.0042
(1.0690) |
0.0064*
(1.9675) |
0.0051
(1.3677) |
0.0076**
(2.4421) |
0.0034
(0.8392) |
| Agriculture Growth | 0.0022***
(3.8005) |
0.0019***
(5.2800) |
0.0021***
(4.6917) |
||
| Services Growth | 0.5485***
(8.5362) |
0.5094***
(8.5219) |
0.6592***
(9.3156) |
||
| Export Growth | 0.0929*
(1.9697) |
0.0401
(1.2310) |
0.0819*
(1.7386) |
0.0541*
(1.9165) |
|
| Import Growth | 0.1856***
(3.3672) |
0.1234***
(2.6379) |
0.1991***
(3.3378) |
0.1107***
(2.9288) |
|
| Credit Growth | 0.0632***
(3.3336) |
0.0125
(0.8320). |
0.0377*
(1.9493) |
0.0010
(0.0758) |
|
| Agri. Growth x Post-Change | -0.0004
(-0.4541) |
-0.0006
(-1.1001) |
-0.0007
(-1.0330) |
||
| Services Growth x Post-Change | -0.1085
(-0.9346) |
-0.1060
(-0.9803) |
-0.0728
(-0.6774) |
||
| Export Growth x Post-Change | -0.0125
(-0.2075) |
0.0024
(0.0449) |
-0.0022
(-0.0368) |
-0.0090
(-0.1851) |
|
| Import Growth x Post-Change | -0.1631**
(-2.4767) |
-0.0965
(-1.5804) |
-0.1866***
(-2.6874) |
-0.0912*
(-1.7305) |
|
| Credit Growth x Post-Change | 0.1260***
(3.6123) |
0.0720**
(2.0397) |
0.1409***
(4.2821) |
0.0847***
(2.6902) |
|
| Constant | 0.0139***
(4.3905) |
0.0026
(1.2230) |
0.0106***
(3.4347) |
0.0006
(0.2944) |
0.0056*
(1.9176) |
| Observations Adjusted R2 | 190
0.5443 |
187
0.7608 |
190
0.6073 |
187
0.7962 |
187
0.7218 |
Note: All columns estimate the following regression: giT=β0 +β1Xi+β1Xi×T+θ1Indiai+θ2Indiai×T+γT+εiT . gi equals the average growth rate for country i in either 2002-11 or 2012-16 period. T equals one for the post-change period and zero otherwise. India equals one for India and zero for all other countries. Columns vary by the choice of covariates used in the model. t-statistics are provided in parentheses. *, ** and *** denote significance levels of 10 per cent, 5 per cent and 1 per cent respectively.
10.22 The solution to omitted variable bias is not as simple as adding more covariates to the model. Thousands of indicators immediately present themselves as candidates, most of which exert their influence on the dependent variable in very indirect, non-linear ways. For example, compared to other countries, India has very high informal sector employment and a large proportion of youth that is not in employment, education or training. Agriculture contributes disproportionately to India’s employment whereas services contributes disproportionately to GDP.
Figure 5: Structural differences between the economies of India and other countries

Source: World Bank WDI database.
Note: Informal sector employment share is a percentage of total non-agricultural employment. Share of youth not in education, employment or training represents the proportion of such individuals aged 15-24 among all individuals aged 15-24. Coal rents as defined by World Bank are the difference between the value of both hard and soft coal production at world prices and their total costs of production. It represents a measure of natural resource contribution to GDP.
10.23 Figure 5 illustrates some of these structural differences between the Indian economy and others. All these variables undoubtedly affect GDP, but in indirect ways that cannot be easily measured or observed.
10.24 A complete model must capture the idiosyncratic drivers of growth of each country in the sample. For example, institutional and legal structures are inherently different across countries, which affect countries in ways that cannot be measured directly. Purnanandam (2019) argues that cross-country regressions of this kind must include country fixed effects to account for such unobserved variations across countries. After controlling for such variation, it finds that the erstwhile mis-estimation of 2.4 per cent in his model disappears altogether.
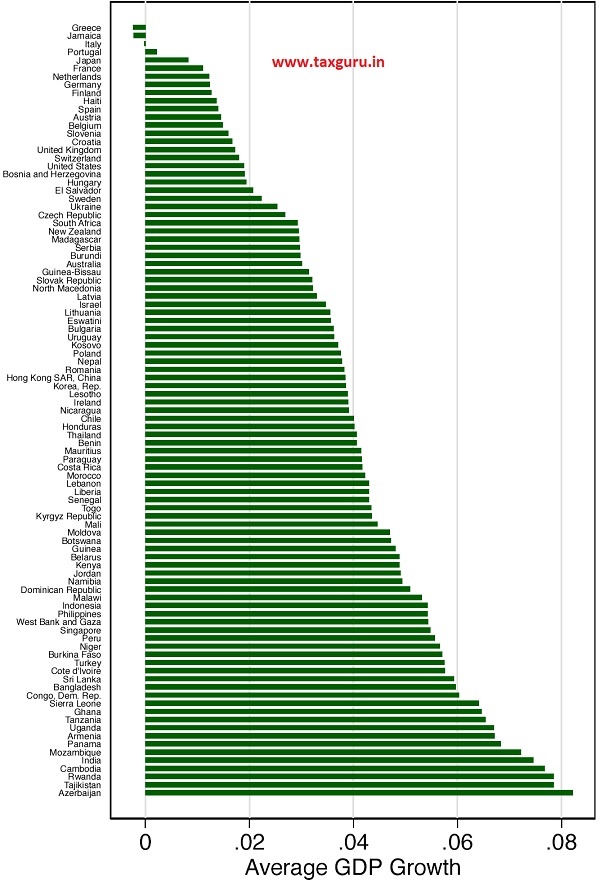
10.25 Figure 6 plots the average growth rate of all countries in the sample over the period 2002-16. Clearly, countries exhibit tremendous variation in their average GDP growth rates. Because average growth rates vary, each country has a different average “effect” on the dependent variable which must be held fixed before it examine the effect of treatment. Put differently, the difference in average growth rates represents important structural differences among countries that must be held fixed before it can examine the effect of treatment. Including country fixed effects in the model achieves exactly this – it accounts for the differences in average growth rates, and by extension all unobserved differences across countries that may influence the dependent variable. Only by including country fixed effects in the model the influence of such unobserved variation can be isolated, counter the omitted variable bias discussed above, and get an unbiased estimate of the effect of treatment.
10.26 In a similar vein, Figure 7 motivates the case for year fixed effects. The chart depicts the cross-sectional average GDP growth of all sample countries in every year from 2002 to 2016. The average is far from constant over time; every year, the sample countries’ average GDP growth behaves differently compared to the previous year. In 2009, the average GDP growth of all sample countries reaches rock bottom owing to the financial crisis – an important factor that affected all countries and therefore must be included in the model as a control. Year fixed effects would control for all such unobserved factors that affect all countries in a given year, and thus take care of another source of omitted variable bias.
10.27 In line with Purnanandam (2019), the baseline specification is modified to include country fixed effects and results are presented in Table 3. As a baseline, the first two columns depict cross-sectional regressions for 200211 and 2012-16 respectively without fixed effects. The variable of interest is the Indiai dummy, which increases from 0.92 per cent pre-change to 3.69 per cent post-change, indicating a mis-estimation of 2.77 per cent, as demonstrated earlier. The third column simply pools the observations in columns 1 and 2, i.e. the pre-change and post-change observations, such that the coefficient of interest now is the interaction between the Indiai dummy and T, the post-change dummy. As earlier, the coefficient reflects the misestimation of 2.77 percent.
10.28 The final column shows the preferred specification that includes country fixed effects, thus implementing a generalized DID model. Here, the coefficient on the India x post-change interaction term turns insignificant. Clearly, a substantial variation in GDP growth is absorbed by unobserved differences across countries, leaving little evidence of any mis-estimation in India’s GDP growth rates.
Figure 6: Need for controlling for difference in average GDP growth across countries
Source: World Bank WDI database.
Figure 7: Need for controlling for difference in global growth rates across years
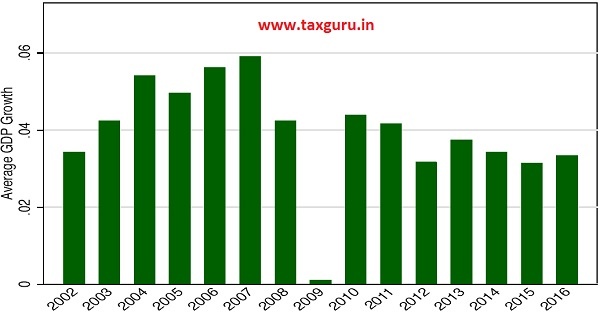
Source: World Bank WDI database.
Table 3: Estimation of abnormal growth with and without controls for differences across countries
| Description of sample: | 2002-11 | 2012-16 | Pooled | Pooled |
| Does the econometric specification control for differences across countries? | No | No | No | Yes and therefore the correct model |
| India | 0.0092**
(2.4151) |
0.0369***
(15.7342) |
0.0092**
(2.4151) |
|
| India x Post-Change | 0.0277***
(6.1757) |
0.0170
(0.9067) |
||
| Post-Change | 0.0042
(1.0690) |
-0.0009
(-0.3852) |
||
| Export Growth Rate | 0.0929*
(1.9697) |
0.0805**
(2.1591) |
0.0929*
(1.9697) |
0.0500
(1.2545) |
| Import Growth Rate | 0.1856***
(3.3672) |
0.0225
(0.6245) |
0.1856***
(3.3672) |
0.0725**
(2.1073) |
| Credit Growth Rate | 0.0632***
(3.3336) |
0.1892***
(6.4593) |
0.0632***
(3.3336) |
0.0756***
(3.7686) |
| Export Growth x Post-Change | -0.0125
(-0.2075) |
|||
| Import Growth x Post-Change | -0.1631**
(-2.4767) |
|||
| Credit Growth x Post-Change | 0.1260***
(3.6123) |
|||
| Constant | 0.0139***
(4.3905) |
0.0181***
(7.7800) |
0.0139***
(4.3905) |
0.0247***
(7.1371) |
| Observations | 95 | 95 | 190 | 190 |
| R2 | 0.5323 | 0.5304 | 0.5443 | 0.6564 |
| Fixed Effects | Country |
Note: Columns 1 and 2 estimate the following cross-sectional regression: gi =/30 +/31Xi +θIndiai +εi. For each country i, the dependent and independent variables are averaged over the period 2002-11 and 2012-16 in columns 1 and 2 respectively. Column 3 pools the observations from both periods and estimates the following regression: giT=/30 +/31Xi+/31Xi×T+θ1Indiai+θ2Indiai×T+γT+εiT. Column 4 also pools the pre-change and post-change observations and includes country fixed effects. gi equals the average growth rate for country i in either 2002-11 or 2012-16 period. T equals one for the post-change period and zero otherwise. India equals one for India and zero for all other countries. t-statistics are provided in parentheses. *, ** and *** denote significance levels of 10 per cent, 5 per cent and 1 per cent respectively.
10.29 The perils of estimating incomplete models without controlling for differences across countries is exemplified in the following experiment. Using baseline specification without country fixed effects, many other countries seems to have misstated their GDPs. Table 4 depicts the results for a subset of these countries. To derive the results in Table 4, now model is re-run with the specifications in columns 3 and 4 of Table 3, with other countries instead of India as the treated group. When the model excludes country fixed effects, many countries appear to have their GDPs overstated or understated, as shown in panels A and B respectively. The over-or under-statement disappears or reduces in magnitude when country fixed effects are introduced in the model. Results reinforce similar findings in other independent studies, notably Bhalla (2019) who finds Germany’s GDP “overstated” and Jamaica’s GDP “understated”, as chapter do, in a model without controls for differences across countries.
10.30 Table 5 shows the results for all the countries in the sample where it was found a “mis-estimation” disappeared after including fixed effects4. These countries amount to more than half of the sample. The average absolute level of what seems to be “misrepresentation” that diminishes after including fixed effects is a massive 1.68 per cent. In the absence of fixed effects, one may erroneously conclude that all the countries in the tables below, including several advanced economies like United Kingdom, Singapore, Germany etc., have flawed methodologies for their respective GDP estimations – an extremely unlikely scenario.
Table 4: Countries with GDP appearing misstated without fixed effects and correction resulting from adding fixed effects (FE)
Panel A: Countries with GDP appearing overstated without country fixed effect
| United Kingdom | Bangladesh | Germany | ||||
| No FE (incorrect) |
FE (correct) | No FE (incorrect) |
FE (correct) | No FE (incorrect) |
FE (correct) | |
| Country x Post-Change | 0.0163***
(4.3289) |
0.0131
(0.7077) |
0.0389***
(8.7502) |
0.0289
(1.5596) |
0.0092**
(2.4795) |
0.0051
(0.2742) |
| Observations | 190 | 190 | 190 | 190 | 190 | 190 |
| R2 | 0.5298 | 0.6552 | 0.5383 | 0.6624 | 0.5315 | 0.6536 |
Panel B: Countries with GDP appearing understated without country fixed effect
| Singapore | South Africa | Belgium | ||||
| No FE (incorrect) |
FE (correct) | No FE (incorrect) |
FE (correct) | No FE (incorrect) |
FE (correct) | |
| Country x Post-Change | -0.0226***
(-8.0765) |
-0.0229
(-1.2451) |
-0.0116***
(-3.6358) |
-0.0130
(-0.6997) |
-0.0135***
(-4.3818) |
-0.0100
(-0.5377) |
| Observations | 190 | 190 | 190 | 190 | 190 | 190 |
| R2 | 0.5334 | 0.6592 | 0.5292 | 0.6552 | 0.5335 | 0.6544 |
Note: For each country, the first column estimates the model: giT=β0 +β1Xi +β1Xi ×T +θ1Countryi +θ2Countryi ×T +γT +εiT. The second column estimates the model: giT =βi +γt +β1XiT +θCountryi ×T +εit, i.e. with country fixed effects. T equals one for the post-change period, i.e. the post-change period, and zero otherwise. Country equals one for the country in question and zero for all other countries. t-statistics are provided in parentheses. *, ** and *** denote significance levels of 10 per cent, 5 per cent and 1 per cent respectively.
Table 5: Countries with GDP appearing misstated without fixed effects and correction resulting from controls for variation across countries
| Country x Post-Change Coefficient | ||||||
| Country | Coefficient without FE (incorrect) | Coefficient with FE (correct) | Is the coefficient significant in FE model? | If yes, whether magnitude lower | Amount of “mis-estimation” corrected (Diff. in coefficients, %) | |
| 1 | Burundi | 0.0404*** | 0.0113 | No | 4.04 | |
| 2 | Bangladesh | 0.0389*** | 0.0289 | No | 3.89 | |
| 3 | Hungary | 0.0385*** | 0.0209 | No | 3.85 | |
| 4 | Romania | 0.0334*** | 0.0187 | No | 3.34 | |
| 5 | Sierra Leone | 0.0309*** | 0.018 | No | 3.09 | |
| 6 | Slovenia | 0.0255*** | 0.0138 | No | 2.55 | |
| 7 | Ghana | 0.0229*** | 0.0021 | No | 2.29 | |
| 8 | United Kingdom | 0.0163*** | 0.0131 | No | 1.63 | |
| 9 | Ireland | 0.0495*** | 0.0338* | Yes | Yes | 1.57 |
| 10 | Kosovo | 0.0152*** | 0.0103 | No | 1.52 | |
| 11 | Kenya | 0.0147*** | 0.0163 | No | 1.47 | |
| 12 | Moldova | 0.0133*** | 0.0042 | No | 1.33 | |
| 13 | Kyrgyz Republic | 0.0130** | 0.0145 | No | 1.30 | |
| 14 | Guinea-Bissau | 0.0123* | 0.0208 | No | 1.23 | |
| 15 | Haiti | 0.0116*** | 0.0185 | No | 1.16 | |
| 16 | Bulgaria | 0.0099** | -0.0006 | No | 0.99 | |
| 17 | Germany | 0.0092** | 0.0051 | No | 0.92 | |
| 18 | Nicaragua | 0.0088** | 0.0197 | No | 0.88 | |
| 19 | Senegal | 0.0079*** | 0.0171 | No | 0.79 | |
| 20 | Spain | 0.0076* | 0.0021 | No | 0.76 | |
| 21 | New Zealand | 0.0058** | 0.0118 | No | 0.58 | |
| 22 | Niger | 0.0598*** | 0.0551*** | Yes | Yes | 0.47 |
| 23 | Congo, Dem. Rep. |
0.0354*** | 0.0339* | Yes | Yes | 0.15 |
| 24 | Azerbaijan | -0.0515*** | -0.0474** | Yes | Yes | -0.41 |
| 25 | Hong Kong SAR, China | -0.0058** | -0.0099 | No | -0.58 | |
| 26 | Philippines | -0.0076** | 0.0045 | No | -0.76 | |
| 27 | Namibia | -0.0091** | -0.0059 | No | -0.91 | |
| 28 | Botswana | -0.0094*** | -0.0037 | No | -0.94 | |
| 29 | Honduras | -0.0095*** | -0.0037 | No | -0.95 | |
| 30 | Finland | -0.0097*** | -0.0092 | No | -0.97 | |
| 31 | Jamaica | -0.0101* | 0.0096 | No | -1.01 | |
| 32 | Serbia | -0.0105*** | -0.021 | No | -1.05 | |
| 33 | Dominican Re- public | -0.0108*** | 0.0031 | No | -1.08 | |
| 34 | South Africa | -0.0116*** | -0.013 | No | -1.16 | |
| 35 | Mauritius | -0.0121*** | -0.004 | No | -1.21 | |
| 36 | Rwanda | -0.0122*** | -0.0118 | No | -1.22 | |
| 37 | Costa Rica | -0.0131*** | -0.0058 | No | -1.31 | |
| 38 | Belgium | -0.0135*** | -0.01 | No | -1.35 | |
| 39 | Burkina Faso | -0.0138** | -0.0078 | No | -1.38 | |
| 40 | Sri Lanka | -0.0146*** | -0.0073 | No | -1.46 | |
| 41 | West Bank and Gaza | -0.0501*** | -0.0349* | Yes | Yes | -1.52 |
| 42 | Slovak Republic | -0.0164*** | -0.0087 | No | -1.64 | |
| 43 | Greece | -0.0187*** | -0.0164 | No | -1.87 | |
| 44 | Nepal | -0.0221*** | -0.0079 | No | -2.21 | |
| 45 | Singapore | -0.0226*** | -0.0229 | No | -2.26 | |
| 46 | Peru | -0.0233*** | -0.0159 | No | -2.33 | |
| 47 | Mali | -0.0241*** | -0.0223 | No | -2.41 | |
| 48 | Jordan | -0.0274*** | -0.0252 | No | -2.74 | |
| 49 | Lebanon | -0.0281*** | -0.0302 | No | -2.81 | |
| 50 | Cambodia | -0.0351*** | -0.0084 | No | -3.51 | |
| 51 | Armenia | -0.0465*** | -0.0306 | No | -4.65 | |
Note: For each country, we estimates two models: giT =β0 +β1Xi +β1Xi ×T +θ1Countryi +θ2Countryi ×T +γT +εiT, and giT =βi +γt +β1XiT +θCountryi ×T +εit, the latter with country fixed effects and the former without. T equals one for the post-change period and zero otherwise. Country equals one for the country in question and zero for all other countries. Continuous variables are averaged over the whole pre- and post-change periods. *, ** and *** denote significance levels of 10 per cent, 5 per cent and 1 per cent respectively. The last column lists the coefficient from the first estimation if the coefficient from the second estimation is insignificant, and the difference between the two coefficients if the coefficient from the second estimation is significant at least at the 10 per cent level.
Panel Data Dynamics: A Modified DID to Account for Country-Specific Trends
10.31 Although the generalized DID model presented in previous section mitigates the risk of omitted variable bias, the analysis must still contend with the parallel trends assumption, which is not fully satisfied in the current sample. If this assumption is not satisfied, at a minimum, one must include a trend line in the specification, as argued in Purnanandam (2019). Baseline model is not amenable to inclusion of a trend line because it has only two time periods – a pre-change and post-change period. However, one can exploit a panel data specification with each country-year treated as an individual observation to implement trend dynamics.
10.32 Purnanandam (2019) shows that in a panel data estimation with country fixed effects, year fixed effects and country-specific trends, the abnormal growth rate obtained in the cross-sectional regressions is completely explained away by differential trend lines across countries. In Table 6, the modified DID model on panel data is estimated by, regressing GDP growth rate on the same independent variables as before but with each country-year treated as an individual observation.
The first column is a baseline without fixed effects or country trends. The results in this column are comparable to a similar panel data specification in Subramanian (2019), with one significant difference – the latter study uses the levels, rather than growth rates, of all variables to establish its results. However, growth rates were chosen because in levels, the variables used in the regression are non-stationary. When variables are growing, a regression in levels can give spurious results (Goyal & Kumar, 2019). In specification, even the baseline model without fixed effects fails to yield a significant coefficient on India x post-change.
10.33 Further, the inclusion of country or year fixed effects to the baseline panel data specification serves to reduce the magnitude of the coefficient of the variable of interest, India x post-change. Lastly, the inclusion of an India trend, or a trend for each country, turns the coefficient negative (although still insignificant)!
Table 6: Estimation of abnormal growth with panel dynamics, including country-specific trends
| No FE | Country FE | Year FE | Country & Year FE | Country & Year FE, India Trend |
Country & Year FE, Country Trends |
|
| India x Post-Change | 0.0221
(1.4838) |
0.0198
(1.4930) |
0.0199
(1.3629) |
0.0166
(1.3057) |
-0.0144
(-0.6535) |
-0.0138
(-0.6522) |
| India | 0.0193**
(2.2456) |
0.0209**
(2.4765) |
||||
| Post-Change | -0.0006
(-0.3777) |
-0.0016
(-1.1147) |
0.0022
(0.6384) |
0.0019
(0.5477) |
-0.0185
(-0.4221) |
|
| India x Time-Trend | 0.0041*
(1.7200) |
|||||
| Export Growth Rate | 0.0670***
(8.1153) |
0.0601***
(7.8152) |
0.0587***
(7.1055) |
0.0471***
(6.2332) |
0.0475***
(6.2844) |
0.0491***
(6.6301) |
| Import Growth Rate | 0.0936***
(11.4934) |
0.0867***
(11.6266) |
0.0839***
(10.3110) |
0.0731***
(10.0078) |
0.0729***
(9.9931) |
0.0703***
(9.5350) |
| Credit Growth Rate | 0.0705***
(13.7564) |
0.0529***
(10.6660) |
0.0645***
(12.5500) |
0.0422***
(8.6036) |
0.0424***
(8.6377) |
0.0355***
(6.8477) |
| Observations | 1349 | 1349 | 1349 | 1349 | 1349 | 1349 |
| Adjusted R2 | 0.3810 | 0.5102 | 0.4050 | 0.5507 | 0.5514 | 0.5897 |
| Country FE | No | Yes | No | Yes | Yes | Yes |
| Year FE | No | No | Yes | Yes | Yes | Yes |
| Time Trend | None | None | None | None | India | Country |
Note: Each column estimates a regression on a panel data of countries with annual data from 2002-2016. Column 1 includes no fixed effects, Column 2 a country fixed effect, Column 3 a year fixed effect and Column 5 both fixed effects. Column 5 includes both fixed effects and a separate time trend for India. Column 6 additionally includes a separate time trend for each country. The dependent variable is the annual growth rate in GDP. t-statistics are provided in parentheses. *, ** and *** denote significance levels of 10 per cent, 5 per cent and 1 per cent respectively.
A DIAGNOSTIC ANALYSIS
10.34 DID models fail to show any misestimation in the Indian GDP. The analysis is concluded by examining other signs that may indicate a problem with the GDP estimation methodology. Subramanian (2019) offers a useful diagnostic, wherein the GDP growth rates are correlated with other indicators that have not undergone any changes in methodology. In essence, the methodology involves correlating the “suspect” variable – the GDP growth rate – with several other “reliable” variables to uncover any suspicious patterns.
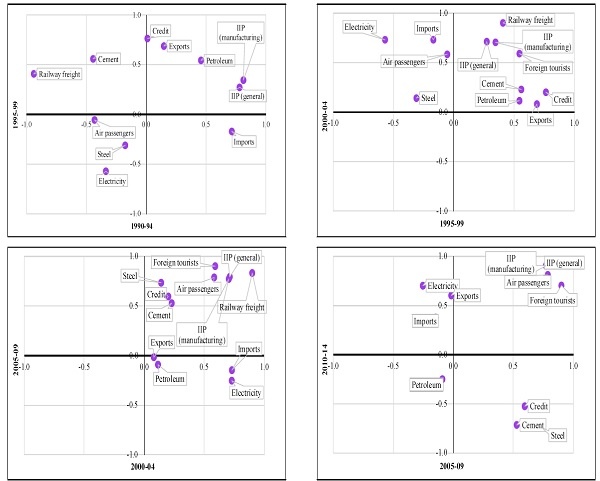
10.35 Figure 8 plots the correlations between GDP growth and several indicators of economic activity in successive five-year periods starting 1980-845. Indeed, over half the correlations change sign in the latest period. But before attributing the counterintuitive signs to the methodology revision in 2011 and resulting mis-estimation of GDP, it is important to check whether these indicators have had a stable and predictable relationship with GDP prior to 2011. However, the relationship between these indicators and GDP growth has been far from stable in the past. The correlations have changed their signs several times even before the 2011 methodology revision. These changes in sign are summarized in Table 7.
10.36 Had these indicators consistently displayed a positive relationship with GDP in the past, making a break from positive to negative only after the methodology revision in 2011, the diagnostic would have yielded a cause for concern. However, the correlations between these indicators and GDP growth have flipped signs in the past even when there were no methodology revisions.
10.37 For example, growth in electricity consumption was negatively correlated with real GDP growth in 1980-84, positively so in 1985-89, negatively so in 1990-99, positively so in 2000-04 and negatively so in 2005-09, flipping signs four times before 2011, the year of methodology revision. Similarly, real exports growth was negatively correlated with GDP growth in 1980-84, positively so in 1985-2004 and negatively so in 2005-09. Figure 9 plots the time-series values of these correlations. Clearly, negative correlations were not at all uncommon in the past. Figure 10 highlights this instability using the standard deviation of these correlations themselves.
Figure 8: Correlation between indicators and GDP growth historically

–
Sources: GDP growth from IMF World Economic Outlook (matches the series used in Subramanian (2019)), sectoral indicators from World Bank WDI database, RBI, and respective Union Ministry databases.
Note: Correlations are computed between the real growth rate in the respective indicator and the real GDP growth rate.
Table 7: Evidence that correlation of sectoral indicator growth with GDP growth has flipped signs many times historically
| Sign of correlation between sectoral indicator growth and GDP growth | |||||||
| Indicator | 1980-84 | 1985-89 | 1990-94 | 1995-99 | 2000-04 | 2005-09 | 2010-14 |
| Exports | – | + | + | + | + | – | + |
| Imports | + | + | + | – | + | – | + |
| Credit | + | – | + | + | + | + | – |
| Electricity | – | + | – | – | + | – | + |
| Petroleum | – | + | + | + | + | – | – |
| Railway freight | + | – | – | + | + | + | |
| Cement | + | + | – | + | + | + | – |
| Steel | – | – | + | + | – | ||
Sources: GDP growth from IMF World Economic Outlook (matches the series in Subramanian (2019)), sectoral indicators from World Bank WDI database, RBI, and respective Union Ministry databases.
Note: Highlighted cells indicate flipping of signs of the correlations before the GDP methodology revision in 2011.
Figure 9: Variation in the correlation between sectoral indicators and GDP growth over time

Sources: GDP growth from IMF World Economic Outlook (matches the series used in Subramanian (2019)), sectoral indicators from World Bank WDI database, RBI, and respective Union Ministry databases.
Figure 10: High volatility in the correlations between indicators and GDP growth
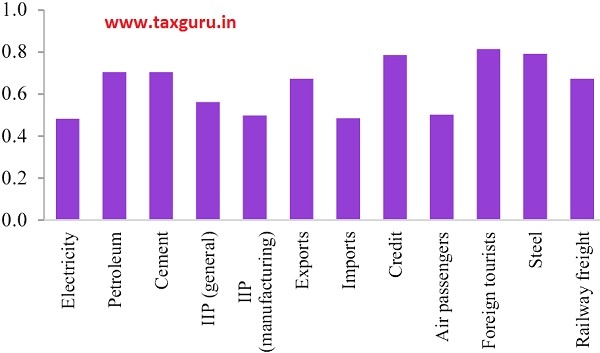
Sources: GDP growth from IMF World Economic Outlook (matches the series in Subramanian (2019)), sectoral indicators from World Bank WDI database, RBI, and respective Union Ministry databases.
Note: For each sector, the correlation between annual sectoral growth and GDP growth was computed in each of twelve 3-year periods: 1980-82, 1983-85, and so on until 2013-15. The chart above depicts the standard deviation of these twelve correlations.
Table 8: GDP growth explained by Subramanian (2019) indicators pre-change: India and other countries
| India | Middle-income countries | All countries | |||||
|
I |
II | III | IV |
V |
|||
| Export Growth Rate | -0.2009
(-0.7939) |
0.0631**
(2.1967) |
0.0431
(1.4057) |
0.0661***
(3.8160) |
0.0398**
(2.3403) |
||
| Import Growth Rate | 0.0870
(0.4671) |
0.1080***
(4.1062) |
0.0747**
(2.3428) |
0.1054***
(6.4254) |
0.0750***
(4.4388) |
||
| Credit Growth Rate | 0.2077
(0.7735) |
0.0598***
(5.2346) |
0.0419***
(4.2707) |
0.0618***
(6.6422) |
0.0392***
(4.8548) |
||
| Constant | 0.0661**
(2.6757) |
0.0286***
(10.8528) |
0.0312***
(7.6420) |
0.0225***
(9.9046) |
0.0254***
(6.9846) |
||
| Observations | 10 | 364 | 364 | 872 | 872 | ||
| R2 | 0.1054 | 0.4125 | 0.5813 | 0.3934 | 0.6293 | ||
| Country FE | No | No | Yes | No | Yes | ||
| Year FE | No | No | Yes | No | Yes | ||
| Clustered by | No | Country | Country | Country | Country | ||
Note: Column I regresses India’s GDP growth rate on its export, import and credit growth rate for the period 2002-11. Column II repeats the regression for all middle-income countries (excluding India) as per World Bank classification, and column IV repeats the regression for all countries (excluding India) in the sample. Columns III and V repeat the regressions in Columns II and IV respectively and additionally include country and year fixed effects. In Columns II through V, standard errors are robust and clustered by country. t-statistics are provided in parentheses. *, ** and *** denote significance levels of 10 per cent, 5 per cent and 1 per cent respectively.
10.38 Given that these indicators do not exhibit a stable relationship with GDP growth even before 2011, they are poorly equipped to diagnose mis-estimation post 2011. This result is more established formally as follows. To test the predictive power of these indicators prior to 2011, the real GDP growth rate was regressed on the real growth in imports, exports and credit for India. For comparison, the analysis repeats the regression for all middle-income countries, and finally repeat the regression for all countries in the sample. The analysis includes observations only from 2002 to 2011 so as to test the explanatory power of the indicators before the methodology revision. Table 8 presents results.
10.39 It is striking that none of the three indicators is statistically significant in explaining GDP growth in India before 2011, even as they assume significance for other countries. Further, only a paltry 10.5 per cent of the variation in Indian GDP growth is explained by these indicators. In contrast, the R2 for other countries ranges from 40 per cent to 63 per cent. The results confirm the inability of these indicators to explain Indian GDP growth even before 2011. The pattern of GDP growth in India is far more complex than what a few indicators of economic activity can predict, and therefore, asserting a mis-estimation based on these indicators alone is inappropriate.
10.40 In its June 2019 report, the Economic Advisory Council to the Prime Minister highlighted the importance of agriculture- and services-based indicators in the diagnostic process (Economic Advisory Council to the Prime Minister, 2019). Therefore, acorrelation chart is plotted below with an alternative set of indicators, this time including indicators from the agriculture and services sectors.
Figure 11: Most agriculture- and services- related indicators correlate positively with GDP growth in 2001-11 and 2012-16

Sources: GDP growth from IMF World Economic Outlook (matches the series in Subramanian (2019)), sectoral indicators from World Bank WDI database, RBI, and respective Union Ministry databases.
Note: Indicators are defined as follows. Agriculture sector indicators include the annual growth rates in production of foodgrains, commercial crops, fisheries, milk and eggs. Manufacturing sector indicators include the annual growth rates in the production of coal, natural gas, N and P205 fertiliser, and IIP (general). Service sector indicators include the annual growth rates in the following: number of originating passengers on the Indian Railways, weight of freight per km moved on Indian roadways, number passengers per km moved on Indian roadways, number of hotel rooms, gross insurance premiums paid, software sales, and spending on restaurants and hotels.
As shown in Figure 11, many indicators were positively correlated with GDP both before and after the methodology revision (notwithstanding the fact that correlations of this kind tend to be inherently unstable and are only naïve predictors of GDP, as argued earlier).
10.41 Given that the correlation between the sectoral indicators of economic activity and GDP growth has been unstable historically, a more useful diagnostic is a comparison of a given indicator’s correlation with the old GDP series and the same indicator’s correlation with the new GDP series. A divergence in the two values would indicate a problem with the new methodology. However, as Figure 12 shows unequivocally, the indicator’s relationship with GDP is broadly unchanged after the methodology revision.
10.42 Figure 12 also suggests that if, instead of 2011, 2010 or 2012 was used as the separating line to catch flips in correlations, the chapter would have arrived at identical results as with 2011 as the separating line. Indeed, a study by Vaidya Nathan (2019) finds, “When we split the data in the paper one year before or after — as pre-2010 and post-2010, or pre-2012 and post-2012 — we get identical results of both flipping and negative correlations,” showing that there is nothing sacrosanct about the year of methodology revision, 2011.
Figure 12: Relationship of indicators with previous GDP series similar to that with the new series

Sources: GDP growth from IMF World Economic Outlook (matches the series in Subramanian (2019)), sectoral indicators from World Bank WDI database, RBI, and respective Union Ministry databases.
Note: Correlation between real sectoral growth and real GDP growth was computed using first the GDP growth under the old methodology with 2004-05 base, then with the GDP growth under the new methodology with 2011-12 base. Both old and new series are available for the years 2001-2011.
Figure 13: Social development indicators
–

Source: Purnanandam (2019)
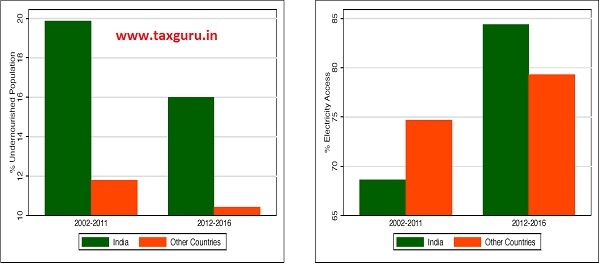
10.43 The analysis in the chapter clearly shows that the evidence in favour of an overstated Indian GDP disappears completely in a correctly specified econometric model. At the same time, more work is needed to fully understand the determinants of India’s growth rate over time. As an illustrative exercise, however, it must be acknowledged that the exact pattern of India’s GDP and how it evolves over time is far from clear. Much more study is required on this important phenomenon. Figure 13 shows a few potential determinants, derived from Purnanandam (2019). India has made impressive improvements in several social development indicators, such as access to nutrition and electricity, that might explain the higher growth rate in Indian GDP in the post-change period. However, it must be acknowledged that the exact pattern of India’s GDP and how it evolves over time is far from clear. Much more study is required on this important phenomenon.
CONCLUSION
10.44 This chapter considers the important issue of the accuracy of India’s GDP estimation. The level and growth of a country’s GDP informs several critical policy initiatives as it is a barometer of the economy’s size and health. It is also a pre-eminent driver of investment. Therefore, it is important that GDP is measured as accurately as possible. Recently, there has been much debate and discussion among scholars, policymakers and citizens alike on whether India’s GDP is estimated correctly.
10.45 If the evidence of a mis-estimation is credible and robust, a radical upheaval of the estimation methodology should follow. However, given the cost of such a massive undertaking, it is important to be certain that there is a need to revisit the estimation methodology. In that spirit, the chapter carefully examines the evidence, leveraging existing scholarly literature and econometric methods to study whether India’s GDP growth is higher than it would have been had its estimation methodology not been revised in 2011. Using a cross-country, generalized difference-in-difference model with fixed effects, the analysis demonstrate the lack of any concrete evidence in favour of a misestimated Indian GDP.
10.46 The larger point made by this chapter needs to be understood by synergistically viewing its findings with the micro-level evidence in Chapter 2, which examines new firm creation in the formal sector across 504 districts in India. Two observations are critical. First, the granular evidence shows that a 10 per cent increase in new firm creation increases district-level GDP growth by 1.8 per cent. As the pace of new firm creation in the formal sector accelerated significantly more after 2014, the resultant impact on district-level growth and thereby country-level growth must be accounted for in any analysis. Along these lines, Purnanandam (2019) shows that India’s improvement in indicators such as access to nutrition and electricity might explain the higher growth rate in Indian GDP post the methodological change. Second, granular evidence on new firm creation shows that new firm creation in the Service sector is far greater than that in manufacturing, infrastructure or agriculture. This micro-level evidence squares up fully with the well-known macro fact on the relative importance of the Services sector in the Indian economy. The need to invest in ramping up India’s statistical infrastructure is undoubted. In this context, the setting up of the 28-member Standing Committee on Economic Statistics (SCES) headed by India’s former Chief Statistician is important. Nevertheless, carefully constructed evidence in the Survey must be taken on board when assessing the quality of Indian data.
CHAPTER AT A GLANCE
> GDP growth is a critical variable for decision-making by investors as well as policymakers. Therefore, the recent debate about whether India’s GDP is correctly estimated following the revision in estimation methodology in 2011 is extremely significant.
> As countries differ in several observed and unobserved ways, cross-country comparisons have to be undertaken with care to separate out the effect of other confounding factors and isolate the effect of the methodology revision alone on GDP growth estimates.
> The models that incorrectly over-estimate GDP growth by 2.7 per cent for India post-2011 also mis-estimate GDP growth over the same time period for 51 other countries out of 95 countries in the sample. Several advanced economies such as UK, Germany and Singapore turn out to have their GDPs misestimated when the econometric model is incompletely specified.
> Correctly specified models that account for all unobserved differences among countries as well as differential trends in GDP growth across countries fail to find any misestimation of growth in India or other countries.
> Concerns of a misestimated Indian GDP are unsubstantiated by the data and are thus unfounded. More broadly, carefully constructed evidence in the Survey, especially that in this chapter combined with micro-level evidence in Chapter 2, must be taken on board when assessing the quality of Indian data.
REFERENCES
Bhalla, S. S. 2019. “Arvind Subramanian’s method suggests Germany overestimates GDP the most.” Financal Express. June 22, 2019. https://www.financialexpress. com/opinion/arvind-subramanians-method-suggests-germany-overestimates-gdp-the-most/1615118/ Cameron, A. C., & Miller, D. L. 2015. “A Practitioner’s Guide to Cluster-Robust Inference”. The Journal of Human Resources, 50(2), 317-372.
Cameron, A. C., Gelbach, J. B., & Miller, D. L. 2008. “Bootstrap-Based Improvements for Inference with Clustered Errors.” The Review of Economics and Statistics, 90(3), 414-427.
Government of India. Economic Advisory Council to the Prime Minister. 2019. GDP estimation in India- Perspectives and Facts. by Bibek Debroy, Rathin Roy, Surjit Bhalla, Charan Singh and Arvind Virmani. New Delhi: Government of India.
Goyal, A., & Kumar, A. 2019. “Indian Growth is Not Overestimated: Mr. Subramanian You Got it Wrong.” WP-2019-019, Indira Gandhi Institute of Development Research.
Goyal, A., & Kumar, A. 2019. “Measuring Indian GDP: Arvind Subramanian Can’t Be Taken Seriously.” Bloomberg Quint. June 20, 2019. https://www.bloombergquint. com/opinion/measuring-indian-gdp-arvind-subramanian-cant-be-taken-seriously
Mazumdar, R. 2019. “World’s Fastest-Growing Economy May Not Be So Fast After All.” Bloomberg. June 11, 2019 https://www. bloomberg.com/news/articles/2019-06-11/ world-s-fastest-growing-economy-may-not-be-so-fast-after-all
Nag, A., & Mazumdar, R. 2019. “India Has Been Accused of Overstating Its Growth Statistics.” Bloomberg. July 25, 2019 https://www.bloomberg.com/news/articles/2019-07-24/india-has-been-accused-of-overstating-its-growth-statistics
Panagariya, A. 2019. “View: Why Arvind Subramanian’s GDP over-estimation argument is flawed.” The Economic Times. June 26, 2019. https://economictimes. indiatimes.com/news/economy/indicators/ view-why-arvind- subramanians -gdp-over-estimation-argument-is-flawed/ articleshow/69949029.cms?from=mdr
Press Trust of India. 2019. “CEA rejects Arvind Subramanian claims, says hard to create wrong narrative.” Livemint. July 4, 2019. https://www.livemint.com/budget/economic -survey/cea-rej ects-arvind-subramanian-claims-says-hard-to-create-wrong-narrative-1562246329862.html
Purnanandam, A. 2019. “Is India’s GDP Growth Rate Really Overstated? A Note.” Stephen M. Ross School of Business, University of Michigan, Ann Arbor, Michigan. July 22, 2019.
Roy, R., & Sapre, A. 2019. “GDP overestimation argument is flawed.” The Hindu BusinessLine. June 19, 2019. https:// www.thehindubusinessline.com/opinion/ gdp-over-estimation-argument-is -flawed/ article28066659.ece#
Shrivastava, R. 2019. “PM’s economic council rejects Arvind Subramanian’s claims on GDP growth over-estimation.” India Today. June 20, 2019. https://www.indiatoday. in/india/story/arvind-subramanian-gst-over-estimation-pm-economic-panel-rebuttal-1552636-2019-06-20
Subramanian, A. 2019 “India’s GDP Mis-estimation: Likelihood, Magnitudes, Mechanisms, and Implications.” Faculty Working Papers No 354. Center for International Development at Harvard University, Cambridge, MA. June, 2019.
Subramanian, A. 2019. “Validating India’s GDP Growth Estimates.” Faculty Working Paper No. 357. Center for International Development at Harvard University, Cambridge, MA. July, 2019.
The Wire. 2019. “ ‘Right Data, Wrong Conclusions’: Modi’s Economic Council Rebuts Subramanian’s GDP Paper.” The Wire. June 19, 2019. https://thewire.in/economy/ arvind-subramanian-pmeac-india-gdp
Vaidya Nathan, K. 2019. “View: What’s wrong with Arvind Subramanian’s GDP math.” The Economic Times. June 17, 2019 https://economictimes.indiatimes.com/news/economy/indicators/view-whats-wrong-with-arvind-subramanians-gdp-math/ articleshow/69816811.cms?from=mdr
Note
1 Net export status of Ghana and Azerbaijan during the sample period being ambiguous, these countries are included in the sample.
2 It was found that by running Subramanian (2019)’s main empirical specification using the sample, India’s GDP is overestimated by 2.77 per cent, which is quite close to the original study’s estimate of 2.5 per cent. This indicates a strong overlap in the samples. Scholarly literature are leveraged to modify the model to take care of additional sources of heterogeneity among the countries in the sample.
3 Standard errors reported in this table and elsewhere, unless explicitly stated otherwise, are unclustered, as the small size of the treatment group (one country only) is insufficient to calculate a robust covariance matrix. Subramanian (2019) reports clustered standard errors in some of his specifications, which may not be suitable given the extremely small number of clusters in the treatment group (see Cameron, Gelbach, & Miller (2008); Cameron & Miller (2015)).
4 For a small number of countries, even though the coefficients are significant even after including country fixed effects, they drop substantially in magnitude.
5 The procedure is in line with Subramanian (2019), who plots the correlations in two periods: 2001-11 and 2012-16. The indicators used in Subramanian (2019) are the growth rates of the following: electricity consumption, 2-wheeler sales, commercial vehicle sales, tractor sales, airline passenger traffic, foreign tourist arrivals, railway freight traffic, index of industrial production, index of industrial production (manufacturing), index of industrial production (consumer goods), petroleum consumption, cement, steel, overall real credit, real credit to industry, exports of goods and services, and imports of goods and services.





